Gallery of WEBGL Minimal Surfaces

This page contains a small gallery of minimal surfaces. If your browser is webgl-enabled (i.e., a recent version of Google Chrome, Firefox or Safari...), you can reach an interactive version of each surface by clicking on the pictures. Short movies are provided in case webgl does not work for you.

	Catenoid and helicoid The first known examples of minimal surfaces (besides the plane), discovered by Leonhard Euler (1744) and Jean Baptiste Meusnier (1776) respectively. If your browser is not webgl-enabled, you can have a look at a movie of the surface.
	Enneper minimal surface(s) Minimal surface(s) discovered by Alfred Enneper (1864). This is an important (family of) algebraic minimal surface(s) with self intersections. The family has an integer parameter, controlling the rotational symmetry group of the surface. If your browser is not webgl-enabled, you can have a look at a movie of the surface.
	Scherk minimal surfaces This family of associated minimal surfaces contains Heinrich Scherk's doubly periodic "chekerboard" minimal surface (1834) and the singly-periodic "saddle tower". If your browser is not webgl-enabled, you can have a look at a movie of the surface.
	A saddle tower with higher symmetry Another singly periodic saddle tower which looks like the desingularized union of 3 planes meeting at 60° angles.
	Catalan minimal surface Minimal surface discovered by E.C. Catalan (1855). It contains a cycloid as a geodesic. If your browser is not webgl-enabled, you can have a look at a movie of the surface.
	Schwarz's P-Surface One of several triply periodic minimal surfaces, discovered by H.A. Schwarz (1890). The unit cell is a cube, and the surface partitions the space into two disjoint, congurent labirynths. If your browser is not webgl-enabled, you can have a look at a movie of the surface.
	Schwarz's D-Surface Another triply periodic minimal surface discovered by H.A. Schwarz (1890). It is the conjugate surface of the P-Surface. The unit cell is again a cube, and the surface partitions the space into two disjoint, congurent labirynths. If your browser is not webgl-enabled, you can have a look at a movie of the surface.
	A. Schoen's Gyroid The only other embedded member of the associate family of the P-Surface and of the D-Surface. Discovered by A. Schoen (1970), proved to be embedded by K. Grosse-Brauchmann and M. Wohlgemuth (1996). This surface contains no segments and there are no symmetry planes. If your browser is not webgl-enabled, you can have a look at a movie of the surface.
	Henneberg minimal surface Minimal surface discovered by L. Henneberg (1876). This surface is non orientable (it contains an embedded Moebius band) and has a Neile's parabola as a geodesic. If your browser is not webgl-enabled, you can have a look at a movie of the surface.
	Richmond minimal surface An algebraic minimal surface with a planar end, discovered by H.W. Richmond (1904). If your browser is not webgl-enabled, you can have a look at a movie of the surface.
	Chen-Gackstatter minimal surface This surface was discovered by C.C. Chen and F. Gackstatter (1982). It looks like an Enneper surface with a handle attached. If your browser is not webgl-enabled, you can have a look at a movie of the surface.
	Jorge-Meeks trinoid minimal surface Discovered by L.P.M. Jorge and W. Meeks III (1983): a beautiful surface with three intersecting catenoidal ends. If your browser is not webgl-enabled, you can have a look at a movie of the surface.
	Costa minimal surface An embedded minimal surface discovered by C. Costa (1984). It looks like the desingularized intersection of a plane and a catenoid. Its discovery gave a whole new life to the research of new embedded minimal surfaces. If your browser is not webgl-enabled, you can have a look at a movie of the surface.
	Morgan minimal surface This is an example, given by F. Morgan (1981), of a Plateau problem whose solution is highly non-unique: there is actually a continuum of (non-minimizing)solutions! If your browser is not webgl-enabled, you can have a look at a movie of the surface.

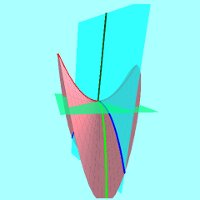Principal curvatures of a surface Minimal surfaces are characterized by the fact that their minimal curvature vanishes identically. The minimal curvature is defined as the arithmetic mean of the principal curvatures. This animation illustrates the concept, showing that normal planes at a given point P cut the surfaces into plane curves called normal sections. Their curvatures at P are called the normal curvatures, and the principal curvatures are the maximum and the minimum of the normal curvatures. Thus, principal curvatures of a minimal surface have equal absolute values and opposite sign at every point.

Variations An animation illustrating variations of a surface: by means of this tool, we can derive the Euler-Lagrange equation for minimal graphs. This shows that a surface having minimal area with respect to its boundary, has vanishing mean curvature.

Gallery of Minimal Surfaces