Statistical classification of Raw Textile defects

The problem of classification of the defects occurring in a textile manufacture is addressed.

A new classification scheme is devised in which different features, extracted from the gray level histogram, shape, and co-occurrence matrices, are employed. All of these features are classified using a Support Vector Machines (SVM) based framework. An accurate analysis of different multi-class classification schemes and SVM parameters has been carried out. The system has been tested using two textile databases, showing very promising results.

Proposed method

The analysis of raw textile images is an important feasible application of the pattern recognition research. In this case, the aim is to automatically detect and classify possible defects occurring in raw textile.

Raw Textile and some possible defects (exist more than 50 different types of Defect)

A new approach is proposed, able to analyze images of raw textiles for finding and classifying the defects in a precise set of typologies. The focus is only on the classification stage, and the defects' detection has been assumed already performed.

The proposed method assumes that the information needed for characterizing the different types of defects can be extracted from the shape, the grey-level intensity, and the texture alteration. Such information is derived by computing from the image three kind of features, extracted from the gray-level histogram, the shape of the defect, and from the co-occurrence matrix.

The proposed approach for Defect Classification

Gray level histogram

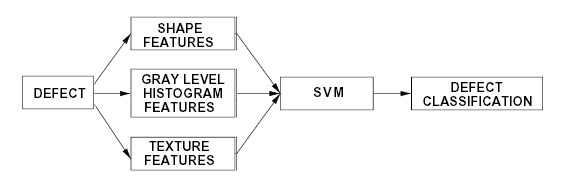
In our approach, a sort of study of the function histogram H(x) has been performed: first, the profile was smoothed by applying a mean filter. Second, a set of features, like max and min values, contrast, etc., are computed.

Shape Descriptors

In the present work, a set of features like area, centroid, major and minor axis length, etc., have been used.

A defect image and his Defect Map from which Shape Descriptors are computed

Co-occurrence matrices

Several gray level Co-occurrence Matrices (CMs) for different values of the dipole have been used. The dipole is defined as a vector D = (alpha,theta), where alpha is the dipole orientation and theta is the length. The length parameter, together with the number of gray levels of the image, is crucial for the effectiveness of the matrix, and strongly depends on the type of the texture under analysis.

Typically, several features are extracted from the CMs, computed for several empirical vectors D, resulting in a large set of often correlated features. In our approach, we propose an alternative use of the co-occurrence matrices, that computes the best dipole length for many orientations for every specific textile analysed, and is able to avoid the feature computation by normalizing CMs to probability density matrices.

Dependence of Statistical Information of CM from Dipole Lenght parameter for one direction and two Textile types.

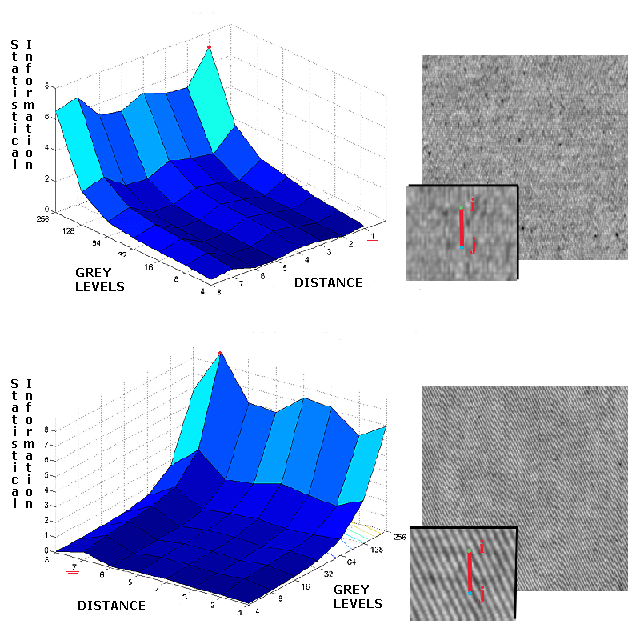
The CM coefficients are directly used as features for the Support Vector Machine architecture. This permits to remove the step of feature computation, which is the major drawback of the technique, giving the task of finding real usuful data in different CM to SVM's training phase.

Classification

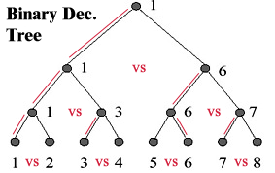
The basic SVM scheme works only for binary classification, and, in order to deal with a multi-class problem, a generalized scheme is introduced. We have compared three schemes:

• SVM 1-vs-R (One versus Rest): this is the standard scheme, which consists in building one SVM for each class Ci, using as negative examples all the patterns of the other classes. An unknown pattern is assigned to the class whose SVM responds positively.
• SVM 1-vs-1 (One versus One): Binary Decision Tree: this method, also called tennis tournament, builds a binary decision tree where each node represents a SVM. The recognition is performed following the rules of a tennis tournament. Each class is regarded as a player, and in each match the system classifies the test defect according to the decision of the SVM trained on the pair of players involved in the match. The winner identities, proposed by each SVM, will be propagated to the upper level of the tree, playing again. The process continues until the root is reached, the winner is the class to be assigned to unknown pattern.
• SVM 1-vs-1 Max Win: this method trains one SVM for each pair of classes. Given an unknown pattern, all SVM are evaluated, counting for each class the number of wins. The pattern is assigned to the class with the maximum number of wins.

The best scheme resulted the SVM 1-vs-1 Binary Decision Tree: this scheme is also the most efficient in terms of time required for training and classification.

Example of the best SVM Classification scheme found.

Experiments

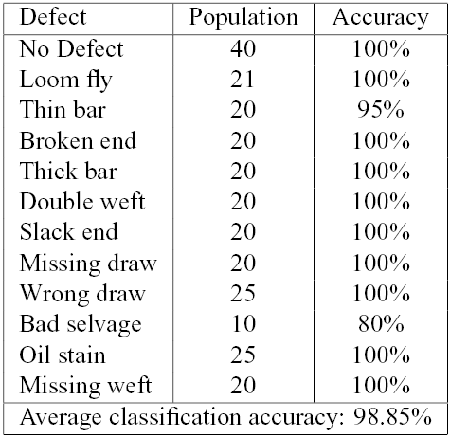
The proposed approach has been tested using two databases:

1. The first one is a Italian Textile Industry database, which contains 2 kinds of textiles, each with 11 and 12 defect classes, respectively. In this case, the orientation of the textile is known.
2. The second one is the TILDA database, realized by the Technische Universität Hamburg in 1995, which consists in 4 different textiles, with a number of defects variable with the considered textile. In this case the orientation of the textile is not known: this is the hardest case, typically disregarded in literature, but crucial from an applicative point of view.

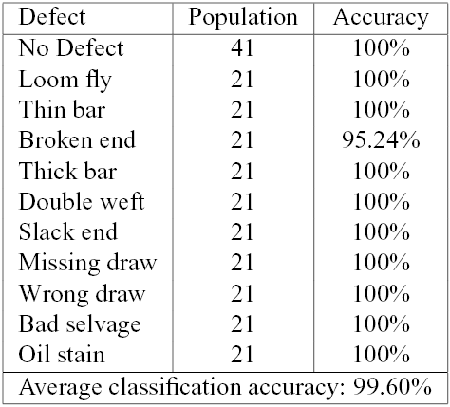
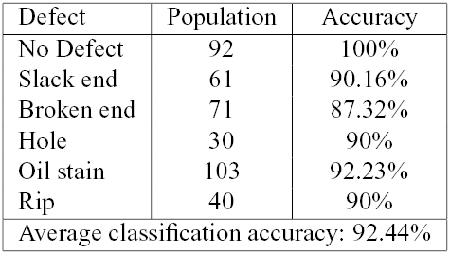
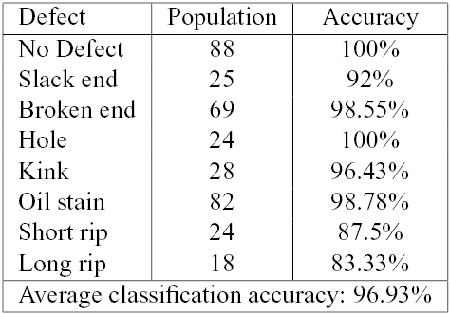
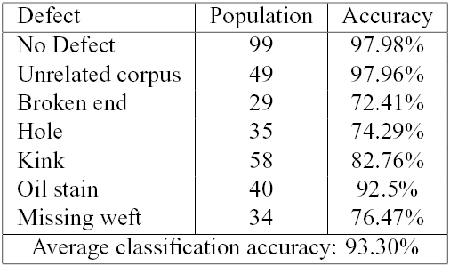
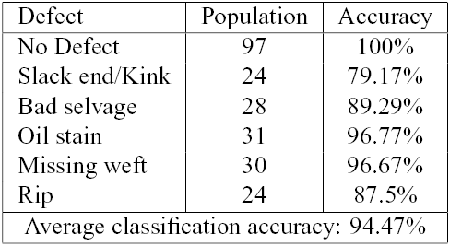
In all cases we have included the class of "No Defect'', in order to validate and refine the defect detection scheme. We have computed the Leave One Out (LOO) error, reporting the results for each class of defect.

The defects nomenclature used derive from Italian Textile Industry and literature.

Classification results of Italian Textile Industry database

Classification results of TILDA database.

Rossi Angelo Ivan (AngeloIvan.Rossi(at)poste.it)