Diario del Corso di Equazioni Differenziali (Modulo B)
Corso di Laurea in Matematica -
Università della Basilicata |
- 7/3/2001 (2 ore): Introduzione agli argomenti del corso.
Richiami sugli spazi di Sobolev (definizioni, Teorema di Meyers-Serrin,
Teoremi di immersione di Sobolev). Enunciato del Teorema di Rellich.
Un criterio di compattezza forte in Lp.
- 8/3/2001 (1 ora): Dimostrazione del teorema di Ascoli-Arzelà.
Dimostrazione del teorema di Rellich.
- 14/3/2001 (2 ore): Conseguenze del teorema di Rellich:
disuguaglianza di Poincaré, caratterizzazione della convergenza
debole in W1,p. Teorema di Meyers-Serrin
e conseguenze. Rapporti
incrementali e loro proprietà.
- 15/3/2001 (1 ora):Caratterizzazione di W1,ploc tramite i rapporti incrementali.
- 21/3/2001 (2 ore): Richiami sulla semicontinuità inferiore.
Funzionali integrali su W1,p: condizioni di crescita,
coercività. Semicontinuità inferiore debole dei funzionali
convessi. Un risultato di semicontinuità inferiore per funzionali
integrali di tipo generale (dipendenti da x,u,Du). Necessità
dell'ipotesi di convessità (costruzione a "zig-zag").
- 22/3/2001 (1 ora): Funzionali quadratici ed equazioni ellittiche in
forma di divergenza: soluzioni deboli e soluzioni forti. Teorema di
Lax-Milgram: esistenza di una soluzione debole quando la matrice dei
coefficienti non è simmetrica.
- 28/3/2001 (2 ore): Disuguaglianza di Caccioppoli. Regolarità
all'interno e fino al bordo per le soluzioni di un'equazione ellittica in
forma di divergenza a coefficienti regolari
(metodo dei rapporti incrementali).
- 29/3/2001 (1 ora): Principio del massimo per soluzioni deboli
di equazioni ellittiche in forma di divergenza. Regolarità dei
minimi di funzionali (non lineari) del calcolo delle variazioni: inizio
dello studio.
- 4/3/2001 (2 ore): Spazi di Morrey Lp,l
e di Campanato
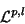 . Isomorfismo di
Lp,l ed . Isomorfismo di
Lp,l ed 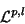 per l<n.
Hoelderianità degli elementi di per l<n.
Hoelderianità degli elementi di 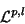 per
n<l<l+p (teorema di Campanato). per
n<l<l+p (teorema di Campanato).
- 6/3/2001 (2 ore): Decadimento della norma L2
delle soluzioni di un'equazione ellittica a coefficienti costanti su palle
concentriche. Regolarità delle soluzioni di un'equazione ellittica a
coefficienti costanti con termine noto in uno spazio di Campanato.
- 24/3/2001 (1 ora): Lemma tecnico di Campanato. Regolarità in
spazi di Morrey delle soluzioni di un'equazione ellittica a coefficienti
continui.
- 26/4/2001 (1 ora): Regolarità hoelderiana (all'interno) per
le soluzioni di un'equazione a coefficienti e termine noto hoelderiani.
Teorema di De Giorgi-Nash-Moser: inizio della dimostrazione delle stime di
Moser.
- 27/4/2001 (2 ore): Stima del sup e dell'inf di una soluzione positiva
in una palla mediante opportuni integrali alla Morrey in palle di raggio
più grande: metodo delle iterazioni di Moser. Se u è
una soluzione, allora log(u) appartiene a BMO. Enunciato del
Lemma di John-Nirenberg e caratterizzazioni di BMO.
- 2/5/2001 (2 ore): Lemma di ricoprimento di Calderon-Zygmund.
Dimostrazione del Lemma di John-Nirenberg. Dimostrazione della
disuguaglianza di Harnack a partire dalle stime di Moser.
- 3/5/2001 (2 ore): Locale hoelderianità come conseguenza
della disuguaglianza di Harnack. Cenni sui sistemi ellittici: stretta
forte ellitticità e condizione di Legendre-Hadamard. Esempio di
forma quadratica che verifica la seconda ma non la prima.
Necessità della condizione di Legendre-Hadamard per la
disuguaglianza di coercività. Sua sufficienza nel caso di
coefficienti costanti o continui (su piccole palle).
- 9/5/2001 (2 ore): Funzioni quasiconvesse. Relazione tra quasiconvessità
e semicontinuità. Esempi di funzioni quasiconvesse non convesse.
Definizione dello spazio BV delle funzioni a variazione limitata.
Esso contiene propriamente lo spazio di Sobolev W1,1.
- 10/5/2001 (1 ora): Variazione totale come misura di Radon. Insiemi
di perimetro finito ed esempi. Semicontinutà della variazione
totale rispetto alla convergenza L1 sugli aperti.
Formula della divergenza generalizzata.
- 16/5/2001 (2 ore): Approssimazione di funzioni BV con
funzioni regolari: enunciato del Teorema di Anzellotti-Giaquinta. Teorema
di compattezza. Variazione totale come inviluppo semicontinuo inferiormente
della norma L1 del gradiente di funzioni regolari.
Regolarizzazione per convoluzione di funzioni BV e sue proprietà.
Dimostrazione del Teorema di Anzellotti-Giaquinta.
- 17/5/2001 (2 ore):Esistenza di insiemi di frontiera minima ("Problema di Plateau"). Formula di coarea per insiemi di perimetro finito.
- 23/5/2001 (2 ore): Approssimazione di insiemi di perimetro finito
con insiemi regolari. Disuguaglianze isoperimetriche. Cenni sulla teoria
delle tracce per funzioni BV. Frontiera ridotta di un insieme di perimetro
finito.
- 24/5/2001 (2 ore): Proprieta' di un insieme di perimetro finito
intorno ad un punto di frontiera ridotta: i blow-up dell'insieme
convergono (in area e localmente in perimetro) al semispazio delimitato
dal piano tangente. Enunciato del teorema di rettificabilità della
frontiera ridotta. Stima della misura di Hausdorff
di sottinsiemi della frontiera ridotta.
|

