28/9/1999 (1 ora):Introduzione al corso.
Misure esterne. Misurabilità secondo Caratheodory.
Proprietà degli insiemi misurabili.
29/9/1999 (1 ora):Esempi di misure esterne.
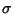 -algebre. Criterio di Caratheodory:
una misura esterna che sia additiva sugli
insiemi con distanza positiva e' una misura di Borel.
-algebre. Criterio di Caratheodory:
una misura esterna che sia additiva sugli
insiemi con distanza positiva e' una misura di Borel.
1/10/1999 (2 ore):Misure definite su una 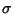 -algebra.
Misure di Borel regolari e misure di Radon. Approssimabilità della misura con
aperti e con compatti. Funzioni misurabili. Funzioni semplici. Approssimazione
di una funzione misurabile non-negativa con funzioni semplici.
-algebra.
Misure di Borel regolari e misure di Radon. Approssimabilità della misura con
aperti e con compatti. Funzioni misurabili. Funzioni semplici. Approssimazione
di una funzione misurabile non-negativa con funzioni semplici.
4/10/1999 (2 ore):Integrale di una
funzione misurabile non negativa.
Teorema della convergenza monotona. Linearità
e proprietà di misura dell'integrale.
Lemma di Fatou e Teorema della convergenza dominata.
8/10/1999 (2 ore):Teorema di Lusin. Spazi normati e spazi di
Banach. Disuguaglianze di Hölder e di Minkowski. Spazi 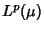 :
sono
spazi normati dopo l'opportuno passaggio a quoziente.
:
sono
spazi normati dopo l'opportuno passaggio a quoziente.
11/10/1999 (2 ore):Teorema di Riesz-Fischer (completezza
degli spazi 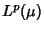 ). Lo spazio
). Lo spazio
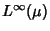 .
Assoluta continuità
dell'integrale. Risultati di densità in
.
Assoluta continuità
dell'integrale. Risultati di densità in
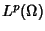 (con
(con
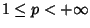 )
delle funzioni limitate e delle funzioni
continue.
)
delle funzioni limitate e delle funzioni
continue.
15/10/1999 (2 ore):Separabilità di
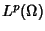 (
(
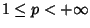 ). Non separabilità di
). Non separabilità di
![$L^\infty([0,1])$](img6.gif) .
Inclusioni tra spazi
.
Inclusioni tra spazi
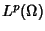 .
Spazi di Hilbert:
.
Spazi di Hilbert:
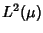 è un esempio. Disuguaglianza di Cauchy-Schwartz. Identità
del parallelogramma. Teorema di proiezione su un convesso chiuso in uno spazio
di Hilbert.
è un esempio. Disuguaglianza di Cauchy-Schwartz. Identità
del parallelogramma. Teorema di proiezione su un convesso chiuso in uno spazio
di Hilbert.
18/10/1999 (2 ore):Controesempi al teorema di proiezione su un
convesso chiuso in un Hilbert quando (a) l'insieme non sia convesso o (b) lo spazio
sia solo di Banach. Decomposizione di uno spazio di Hilbert in somma diretta di
un suo sottospazio chiuso e del suo ortogonale. Duale di uno spazio normato:
equivalenza tra continuità e lipschitzianità di un funzionale lineare. Norma
duale. Duale degli spazi 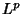 (senza dimostrazione).
Enunciato del teorema sul duale di uno spazio di Hilbert.
(senza dimostrazione).
Enunciato del teorema sul duale di uno spazio di Hilbert.
22/10/1999 (2 ore):Duale di uno spazio di Hilbert.
Sistemi ortonormali. Disuguaglianza di Bessel. Basi di Hilbert e teorema di
Riesz-Fischer sulle serie di Fourier astratte. Serie di Fourier trigonometriche
in 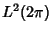 .
.
29/10/1999 (2 ore):Teorema di Baire. Teorema di Banach-Steinhaus
(o principio dell'uniforme limitatezza). Applicazione alle serie di Fourier:
esistono ``moltissime'' funzioni continue e
periodiche la cui serie di Fourier non converge in qualche punto.
5/11/1999 (2 ore):Lemma di Riesz. La palla unitaria 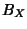 di uno spazio normato di dimensione infinita
di uno spazio normato di dimensione infinita 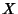 non è mai compatta.
Topologia debole e convergenza debole. Una successione debolmente convergente
è limitata.
Esempi negli spazi
non è mai compatta.
Topologia debole e convergenza debole. Una successione debolmente convergente
è limitata.
Esempi negli spazi 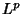 .
Convergenza
debole in uno spazio di Hilbert separabile: corrisponde alla convergenza
``componente per componente'' (rispetto ad una data base di Hilbert).
Compattezza debole della palla unitaria di uno spazio di Hilbert separabile.
.
Convergenza
debole in uno spazio di Hilbert separabile: corrisponde alla convergenza
``componente per componente'' (rispetto ad una data base di Hilbert).
Compattezza debole della palla unitaria di uno spazio di Hilbert separabile.
8/11/1999 (2 ore):Teorema di Hahn-Banach. Funzionale di
Minkowski di un intorno convesso aperto dell'origine. Conseguenza geometrica
del Teorema di Hahn-Banach: due convessi non vuoti e disgiunti, uno dei quali
aperto, si separano con un iperpiano affine.
12/11/1999 (2 ore):Seconda conseguenza geometrica del Teorema di
Hahn Banach: due convessi disgiunti e non vuoti, uno dei quali compatto e l'altro
chiuso, si separano in senso stretto con un iperpiano affine. Corollario: un
insieme convesso fortemente chiuso è anche (sequenzialmente) debolmente chiuso,
ed una funzione convessa fortemente semicontinua inferiormente è anche
(sequenzialmente) debolmente semicontinua. L'iniezione canonica di uno spazio
di Banach 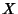 nel suo biduale
nel suo biduale 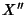 è isometrica. Spazi riflessivi.
Enunciato del teorema di compattezza sequenziale debole della palla di uno spazio di
Banach riflessivo e separabile. Teorema di proiezione su un chiuso convesso in uno
spazio di Banach riflessivo e separabile.
è isometrica. Spazi riflessivi.
Enunciato del teorema di compattezza sequenziale debole della palla di uno spazio di
Banach riflessivo e separabile. Teorema di proiezione su un chiuso convesso in uno
spazio di Banach riflessivo e separabile.
15/11/1999 (1 ora):Il duale di
![$L^\infty([-1,1])$](img13.gif) non è
non è
![$L^1([-1,1])$](img14.gif) .
Dimostrazione del teorema di compattezza sequenziale debole per la palla
chiusa di uno spazio di Banach riflessivo il cui duale sia separabile.
.
Dimostrazione del teorema di compattezza sequenziale debole per la palla
chiusa di uno spazio di Banach riflessivo il cui duale sia separabile.
19/11/1999 (1 ora):Continuità delle traslazioni in
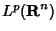 (
(
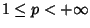 ).
Approssimazione per convoluzione in
).
Approssimazione per convoluzione in
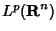 (
(
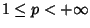 ). Richiami sul teorema di Fubini e sulla
derivazione sotto il segno di integrale.
). Richiami sul teorema di Fubini e sulla
derivazione sotto il segno di integrale.
22/11/1999 (2 ore):Lo spazio di Sobolev
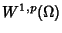 :
definizione, unicità delle derivate deboli. Il caso
:
definizione, unicità delle derivate deboli. Il caso
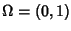 :
ogn elemento
di
:
ogn elemento
di
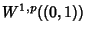 coincide quasi ovunque con una funzione assolutamente continua,
la cui derivata coincide con la derivata debole. Lo spazio
coincide quasi ovunque con una funzione assolutamente continua,
la cui derivata coincide con la derivata debole. Lo spazio
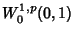 :
definizione, stime hölderiane e risultato di compattezza.
Esempio di una funzione di Sobolev
discontinua in un aperto di
:
definizione, stime hölderiane e risultato di compattezza.
Esempio di una funzione di Sobolev
discontinua in un aperto di 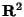 .
Norma negli spazi di Sobolev:
.
Norma negli spazi di Sobolev:
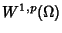 è
uno spazio di Banach,
è
uno spazio di Banach,
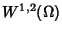 è uno spazio di Hilbert.
è uno spazio di Hilbert.
26/11/1999 (2 ore):Teorema di Meyers-Serrin: densità delle funzioni
regolari in
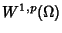 .
Lo spazio
.
Lo spazio
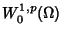 .
Esistenza di una
soluzione debole dell'equazione
.
Esistenza di una
soluzione debole dell'equazione
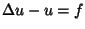 in
in
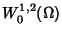 .
Disuguaglianza
di Poincaré in
.
Disuguaglianza
di Poincaré in
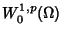 .
.
29/11/1999 (1 ora):Soluzione debole in
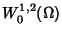 dell'equazione ellittica in forma di divergenza
dell'equazione ellittica in forma di divergenza
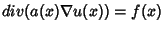 ,
dove il termine noto
,
dove il termine noto 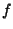 è in
è in
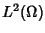 ,
e la matrice
,
e la matrice 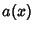 è simmetrica ed uniformemente
ellittica. Enunciato del teorema di immersione di Sobolev nel caso
è simmetrica ed uniformemente
ellittica. Enunciato del teorema di immersione di Sobolev nel caso 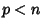 .
Considerazioni euristiche sull'esponente di Sobolev.
.
Considerazioni euristiche sull'esponente di Sobolev.
3/12/1999 (2 ore):Lemma di Gagliardo. Teorema di immersione
di Sobolev nel caso 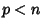 per lo spazio
per lo spazio
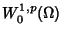 .
Teorema di immersione di Sobolev (teorema di Morrey)
nel caso
.
Teorema di immersione di Sobolev (teorema di Morrey)
nel caso 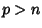 per lo spazio
per lo spazio
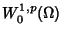 . Estensione dei teoremi di
immersione
a
. Estensione dei teoremi di
immersione
a
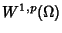 nel caso in cui
nel caso in cui 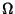 abbia frontiera regolare (senza
dimostrazione).
abbia frontiera regolare (senza
dimostrazione).
6/12/1999 (1 ora):Spazi
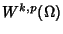 e relative estensioni del
teorema di immersione di Sobolev. Teorema di Rellich (solo enunciato) e compattezza
debole in
e relative estensioni del
teorema di immersione di Sobolev. Teorema di Rellich (solo enunciato) e compattezza
debole in
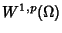 .
Caratterizzazione degli spazi
.
Caratterizzazione degli spazi
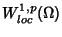 tramite i rapporti incrementali.
tramite i rapporti incrementali.
10/12/1999 (2 ore):Dimostrazione della caratterizzazione di
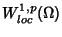 tramite i rapporti incrementali. Disuguaglianza di
Caccioppoli per le soluzioni deboli in
tramite i rapporti incrementali. Disuguaglianza di
Caccioppoli per le soluzioni deboli in
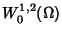 dell'equazione
dell'equazione
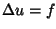 .
Regolarità all'interno per la stessa equazione. Cenni sulla
soluzione variazionale di problemi ellittici.
.
Regolarità all'interno per la stessa equazione. Cenni sulla
soluzione variazionale di problemi ellittici.
Bibliografia.
- [1]
- H. Brezis: Analisi Funzionale. Teoria e applicazioni. Napoli,
Liguori 1986.
- [2]
- E. Giusti: Metodi diretti nel Calcolo delle Variazioni.
Unione Matematica Italiana, Bologna, 1994.
- [3]
- L.C. Evans, R.F. Gariepy: Measure theory
and fine properties of functions.
Studies in Advanced Mathematics, CRC Press, Boca Raton 1992.
- [4]
- E. Giusti: Minimal Surfaces and Functions of Bounded Variation,
Birkhäuser, Boston 1984.
- [5]
- W. Rudin: Real and complex analysis, Tata Mc Graw-Hill, New Delhi,1974
- [6]
- M. Giaquinta: Introduction to Regularity
Theory for Nonlinear Elliptic Systems, Lectures in
Mathematics ETH Zuerich, Birkhaeuser, Basel 1993.

